RaMBO: Ranking Metric Blackbox Optimization
Published:
(authored by Marin Vlastelica)
Our paper resulting in an oral at CVPR 2020 about applying the blackbox differentiation theory (codename #blackboxbackprop) to optimizing rank-based metrics. As it turns out, it is all possible with a few simple twists…
In our newest paper [1] we are dealing with training of deep neural networks by directly **optimizing rank-based metrics. Our approach bases itself on the blackbox-backprop theory introduced in [2]. In the blackbox-backprop paper (see **#blackboxbackprop **on Twitter for latest updates and the accompanying blogpost), we have shown how to calculate “useful” gradients through combinatorial solvers in neural networks, without hurting the optimality of the solvers themselves. The theory enables us to utilize the **combinatorial **solvers as plug and play modules **within complicated models which we can train with the standard backpropagation algorithm.
In search for practical application of the theory, we turn to computer vision. Concretely, we show that applying blackbox-backprop to computer vision benchmarks for **optimizing recall and Average Precision **for retrieval and detection tasks consistently improves the underlying architectures’ performance. This is, by the way, a common theme in ML, that it is always desirable to optimize for what you actually care for. If the recall@K is the right measure of performance, then it makes sense to make the end-to-end architecture optimize that and not some sort of approximation. Both recall (more concretely, recall@K) and Average Precision are metrics that are based on rankings of the inputs, which essentially require a sorting operation of their scores. Here, multiple things pose a challenge. For one, using these metrics as loss functions results in non-decomposable losses (i.e. we cannot reliably estimate the loss based on the subset of the input, but we require the whole set of inputs). Additionally, the ranking operation that is used to calculate the metrics is non-differentiable.
Although many competing approaches have been proposed, they have not been accepted by the practitioners for different reasons. They’re computationally too expensive or were lacking practical implementations for easy use. With the blackbox-backprop theory, we apply the sorting operation directly on the outputted scores, which results in low computational complexity O(n log n) (the complexity of general sorting with** torch.argsort**). The questions that we need to answer are the following:
How to cast the ranking problem into the blackbox differentiation framework?
How to address the non-decomposability of the losses?
How to prevent rank-based losses from collapsing?
Fitting Ranking into the Blackbox Differentiation Framework
In order to cast ranking into the framework proposed in [2], we need an argmin operation over a dot product. We first define the vector of scores, y. The ranking of y, rk(y) is the result of an argmin operation on the dot product between the vector **y **and permutation **π, **over the set of all possible permutations:
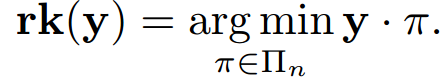
The proof of the previous proposition is simple and based upon the well-known permutation inequality which states that given a decreasing sequence (the vector y), for any integer n:
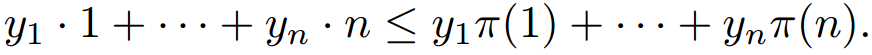
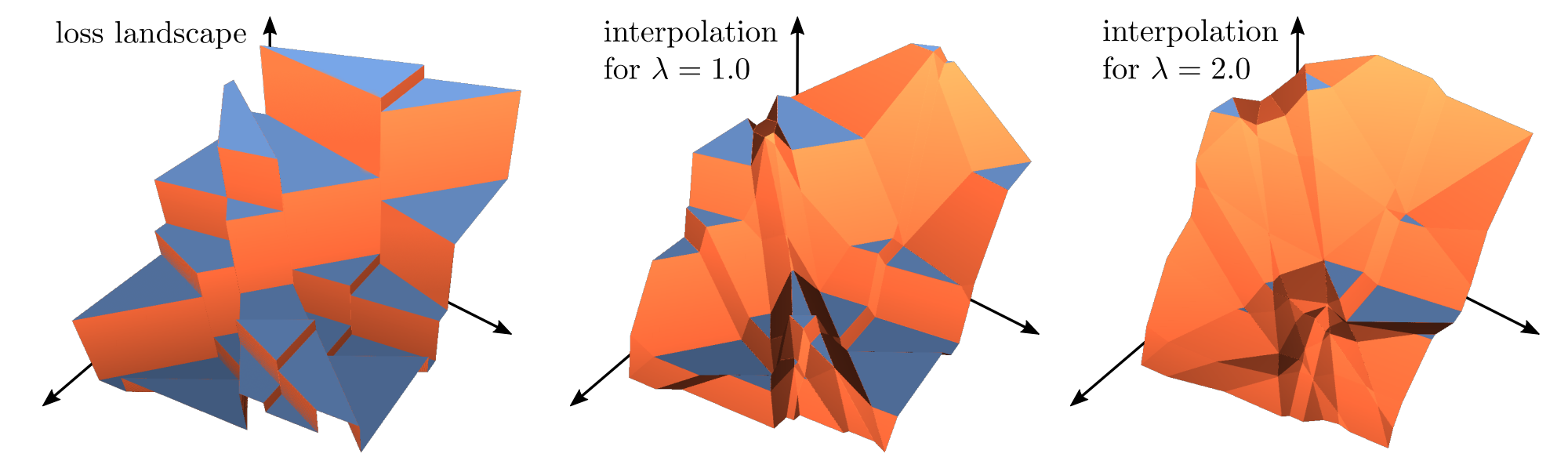
Intuitively, this means that the least weight is put on the biggest scores, which happens if the permutation is a sorting permutation. With this simple twist, we are able to apply the blackbox framework to the ranking problem, this means that we can simply use an efficient implementation of a fast sorting algorithm (torch.argsort in PyTorch for instance) in order to calculate the ranking and differentiate through it** based on the blackbox-backprop theory. **An example of the optimization landscape resulting from applying the blackbox-backprop theory can be seen in the following figure:
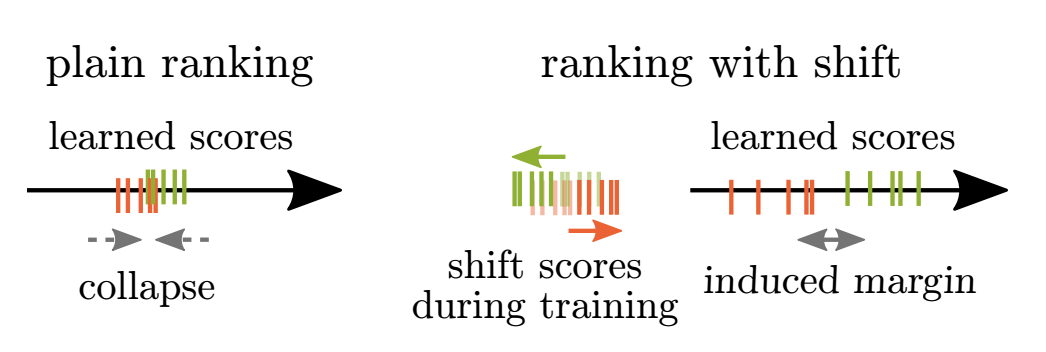
Score Margin to Prevent Loss Collapse
Rank-based losses have a difficult time dealing with ties. To illustrate their instability, think of the situation where we have a tie over the whole dataset in scores. We can obtain all possible rankings in a small neighborhood of such a tie, since the smallest change to scores changes the ranking completely. This means that applying rank-based losses is very unstable. We alleviate the problem by** introducing a margin α** inducing a positive shift on the negatively labeled scores and a negative shift on the positively labeled scores:
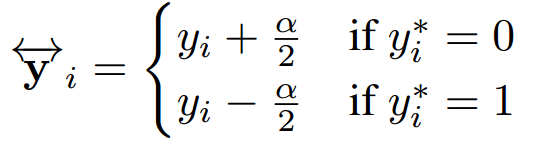
Score Memory for Better Estimates
Ideally, we would have a dataset-wide loss to optimize, because of the non-decomposability problem of the ranking-based losses. Because this is computationally intractable (as it is limited by GPU memory for example), we want to use minibatches to train our models. We allow for this by extending the scores of the current batch with scores of a certain number of previous batches, which reduces the bias of the loss estimate.
The Algorithm
Taking the above mentioned techniques yields a method that we call Ranking Metric Blackbox Optimization (RaMBO). Again, the additional computational overhead is introduced only by the complexity of the** sorting operation** O(n log n), which is blazing fast when implemented efficiently. This puts us ahead of most approaches out there. The algorithm is summarized in the following listing:

We evaluated the performance of our approach on object detection (Pascal VOC) and several image retrieval benchmarks (CUB-200–2011, In-shop Clothes, Stanford Online Products). In each experiment, we take well-performing architectures and modify them with RaMBO. The method is on-par or beats the state-of-the-art results in these benchmarks.
Nevertheless, we should acknowledge that metric learning baselines are a mess, as a result of a fast and enormous body of research in different directions (improving network architectures, better objective functions and so forth). This leads to irreproducible results, wrong conclusions and unfair comparisons, a great analysis of these difficulties can be found here.
 Stanford Products dataset for retrieval.
Stanford Products dataset for retrieval.
References
[1] Rolínek, Michal et al. Optimizing Rank-based Metrics with Blackbox Differentiation, CVPR 2020
[2] Vlastelica, Marin et al. Differentiation of Blackbox Combinatorial Solvers, ICLR 2020
[3] Images taken from Pixabay
Acknowledgments
This is joint work from the Autonomous Learning Group of the Max Planck Institute for Intelligent Systems, Tuebingen, Germany, the Univesity of Tuebingen and Universita degli Studi di Firenze, Italy.
